The Cell Modeling Lab at Duke-NUS

Research on Mathematical Modeling in Cancer Biology

The Tucker-Kellogg lab at Duke-NUS uses mathematical modeling to study problems in the molecular biology of cancer, especially problems of combination therapy and drug-resistance. We use graphical models, ODE models, and agent-based simulations to study dynamic cellular phenomena such as phenotypic plasticity, pathway activation, proliferation rates, and metabolic change.

Mathematical equations are simply a language for describing what we know. Computational simulations are simply a technique for repeating and scaling up things we already know, so we can describe situations that would be too complicated to hold in mind at one time.

Methods from population dynamics help us study clonal expansion and the evolution of subpopulations of cells that resist drugs or combinations of drugs.
Markov models can decribe the stochastic transitions of cell state, such as mutations or phenotype changes, as they interact with exponential processes like proliferation or drug-killing.
Models with ordinary differential equations can decribe the timing and magnitude of activation and inhibition relationships in interdependent systems, such as biochemical networks.
Models of metabolic flux can analyze snapshot datasets that measure abundance, and provide useful interpretations about pathway utilization.

Overall, these approaches allow integration of isolated facts and scale-up of cause-and-effect reasoning, to examine different hypothesis for complex cellular behaviors. We collaborate with experimental partners to create back-and-forth between modeling and experiments.

Cancer Evolution of Drug Resistance

Effect of synergistic drug combinations on the Evolution of cancer drug resistance

Synergistic drug combinations are widely preferred in cancer therapy because they exhibit enhanced therapeutic efficacy at lower doses. Although synergism is intuitively attractive, therapeutic success often depends on whether drug resistance develops. We used a simplified computational model of cancer cell numbers in a population of drug-sensitive, singly-resistant, and fully-resistant cells to simulate the dynamics of resistance evolution in the presence of two-drug combinations. Computational simulations show that if different combination therapies have similar initial efficacy in cancers, then nonsynergistic drug combinations are more likely than synergistic drug combinations to provide a long-term defense against the evolution of therapeutic resistance [Saputra et. al., Cancer Research 2018 ].

When we compared combination therapies administered at the same combination of effective doses, simulations showed synergistic combinations most effective at delaying onset of resistance. Paradoxically, when the therapies were compared using dose combinations with equal initial efficacy, antagonistic combinations were most successful at suppressing expansion of resistant subclones. These findings suggest that, although synergistic combinations could suppress resistance through early decimation of cell numbers (making them “proefficacy” strategies), they are inherently fragile toward the development of single resistance. In contrast, antagonistic combinations suppressed the clonal expansion of singly-resistant cells, making them “antiresistance” strategies. The distinction between synergism and antagonism was intrinsically connected to the distinction between offensive and defensive strategies, where offensive strategies inflicted early casualties and defensive strategies established protection against anticipated future threats.

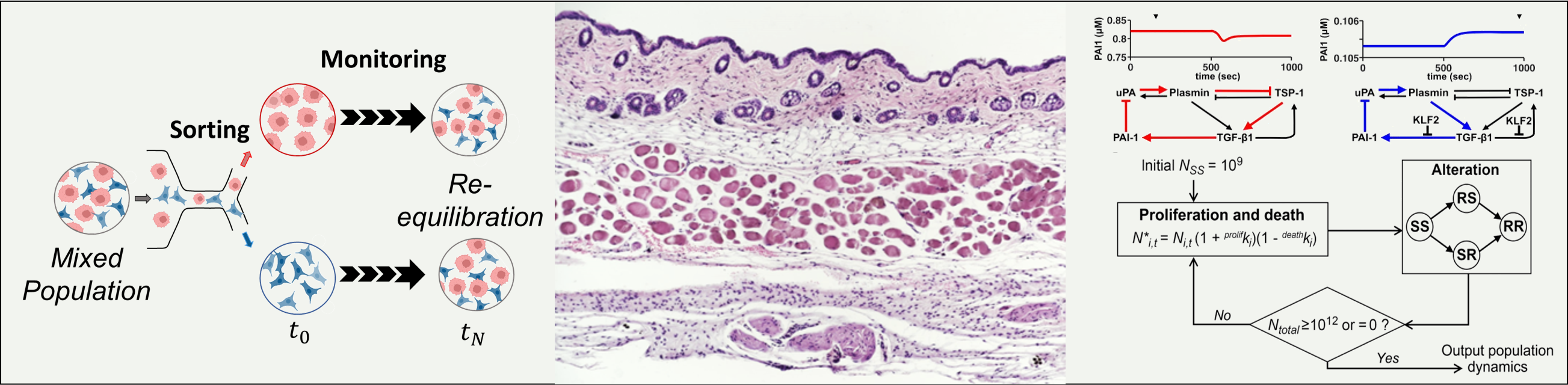
Studying phenotypic plasticity in tumor populations

Gradual population-level changes in tissues can be driven by stochastic plasticity, meaning rare stochastic transitions of single-cell phenotype. Quantifying the rates of these stochastic transitions requires time-intensive experiments, and analysis is generally confounded by simultaneous bidirectional transitions and asymmetric proliferation kinetics. To quantify cellular plasticity, we developed Transcompp (Transition Rate ANalysis of Single Cells to Observe and Measure Phenotypic Plasticity), a Markov modeling algorithm that uses optimization and resampling to compute best-fit rates and statistical intervals for stochastic cell-state transitions [Jagannathan et. al., Bioinformatics 2020 ].

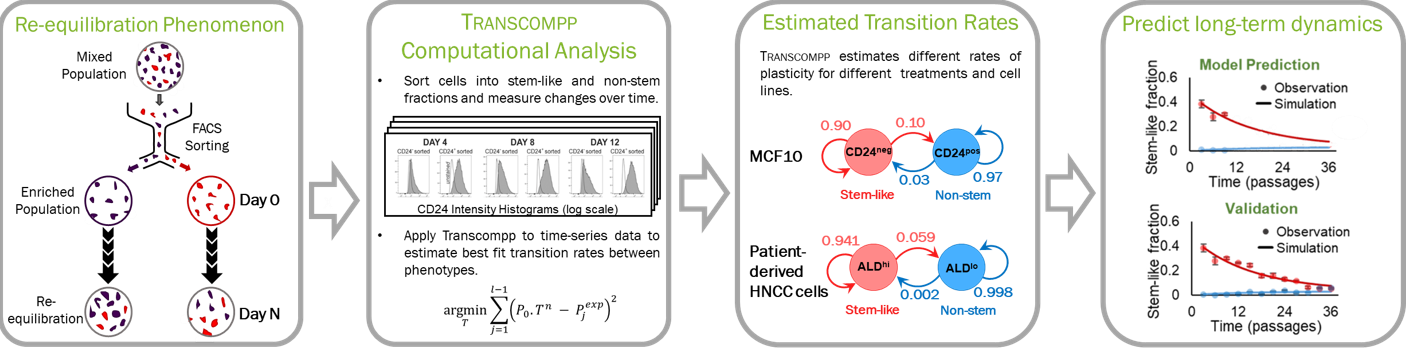
We applied Transcompp to time-series datasets in which purified subpopulations of stem-like or non-stem cancer cells were exposed to various cell culture environments, and allowed to re-equilibrate spontaneously over time. Results revealed that commonly used cell culture reagents hydrocortisone and cholera toxin shifted the cell population equilibrium toward stem-like or non-stem states, respectively, in the basal-like breast cancer cell line MCF10CA1a. In addition, applying Transcompp to patient-derived cells showed that transition rates computed from short-term experiments could predict long-term trajectories and equilibrium convergence of the cultured cell population.